Estimados seguidores, a lo largo de nuestra ya lejana escolaridad obligatoria, alguna que otra vez nos hemos topado con singulares números irracionales (no se pueden expresar como fracción): el número pí (Π), el número (e) número de oro, áureo o divina proporción phi (Φ) entre los más destacados y dependiendo del curso trabajado.
En estas breves líneas quiero destacar la importancia que ha tenido y sigue teniendo actualmente la proporción divina en los distintos campos: arquitectura, arte, ciencias naturales, logotipos de empresas, …
¿Φ aparece o está ahí para ser descubierto? En el siglo XII un matemático italiano, Fibonacci creó la siguiente sucesión: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … si observamos cada término se construye sumando los dos anteriores y además el cociente de dos términos consecutivos se va aproximando a la cantidad: 1,6180339887…
Que es solución de la ecuación: x2 -x -1=0
Puedes comprobarlo en este mismo instante con la calculadora del móvil: Por ejemplo: 21/13: 1,615348…; 233/144= 1,618055… Cuando nos acercamos al término cuadragésimo de la sucesión, el cociente se aproxima al número áureo: Φ=1,6180339887…
En la naturaleza y concretamente en las flores de girasol, podemos encontrar que el número de pepitas en sentido horario/antihorario tienen relación con pares de números pertenecientes a la serie de Fibonacci. También se ha observado esta relación en el número de pétalos de muchas flores, ramas de árboles e incluso en la forma de las hojas. Otra curiosidad de nuestra vida cotidiana sería el por qué de las dimensiones de carteras; bolsos; tarjetas de crédito o de visitas; carnés de distintos estamentos, las dimensiones de la pantalla de un tv, formato de algunos libros de bolsillo, logos, edificios, cuadros …
La mayoría de ellos tienen la misma forma y proporción, son los llamados rectángulos áureos (RA), la relación entre sus lados debe ser Φ. El rectángulo áureo tiene de lados 1 y Φ.
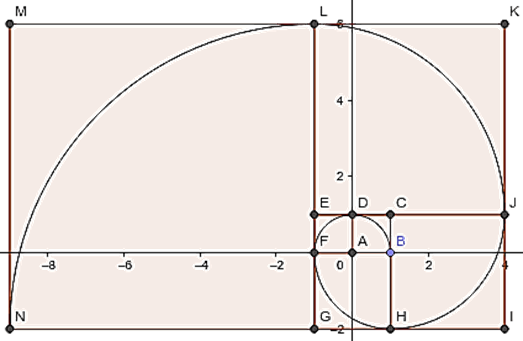
Otra de las curiosidades con las que nos sorprende la proporción divina se encuentran en la espiral áurea (EA), de Fibonacci o logarítmica. Podemos encontrarla en cuerpos pequeños como las escamas de una piña, flora de la alcachofa, ramas de los árboles, conchas del Nautilus pompilius, oreja humana … y en cuerpos enormes como en los huracanes y galaxias.
Esta espiral la obtenemos partiendo de un RA como el de la figura; vamos dibujando dentro de él cuadrados y dibujamos el arco correspondiente con radio igual al cuadrado donde se encuentra. Pueden dibujarla en un folio y a mano alzada.
Durante la época del Renacimiento, se empezaron a buscar nuevas técnicas para el desarrollo de la perspectiva y de las proporciones ideales y así lograr plasmar la belleza de la naturaleza humana; es el comienzo de la geometría proyectiva. Maestros como Leonardo da Vinci, Rafael Sanzio o Alberto Durero fueron los precursores y conseguidores de esta técnica, plasmar de manera realista los objetos de 3D en 2D. Como ejemplo tenemos la utilización de los rectángulos y espirales áureas en las obras de La última cena y La Gioconda de Leonardo.
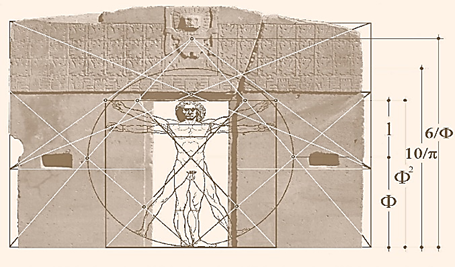
También la proporción áurea podemos descubrirla en la arquitectura desde los antiguos egipcios, por ejemplo la altura y la base de la pirámide de Keops guardan entre sí una incondicional correspondencia con Φ. Los arcos de triunfo de la Roma clásica siguen la proporción áurea, como también lo hacen las tumbas licias y las iglesias de la antigua ciudad de Mira, actualmente Demre (Turquía). La arquitectura preincaica del continente americano sigue fielmente Φ. La construcción del 1500 a.C., La Puerta del Sol de Tiwanaku cercana al lago Titicaca (Bolivia), presenta una composición que parece estar articulada por rectángulos áureos. En la imagen podemos observar cómo se inscribe perfectamente la figura del hombre ideal (Venecia) realizada sobre el siglo I a.C. por Vitruvio, arquitecto de Julio César.
Dejo para el final el ejemplo más representativo del seguimiento fiel de la proporción divina: el Partenón de Atenas de Fidias que dio nombre a nuestro excitante número phi (Φ).
Los diseñadores gráficos también buscan la perfección matemática (áurea) en el diseño de logotipos de pequeñas y grandes empresas. Su uso genera una proporcionalidad natural ante el espectador que es necesaria para obtener una visual con armonía. La diseñadora gráfica rusa Florian Popescu se dedicó a la tarea de encontrar secciones áureas y demás elementos geométricos y matemáticos en la identidad visual de diferentes marcas famosas. A partir de la lectura de este artículo miraremos de otra manera y las imágenes que nos llamen extrañamente la atención y que no nos cuadren; seguro que no guardan la divina proporción.