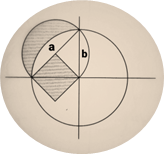
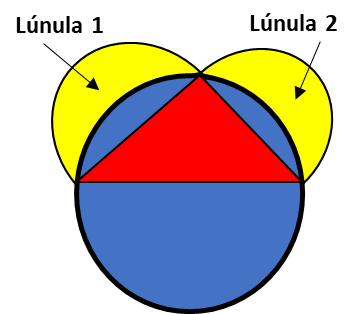
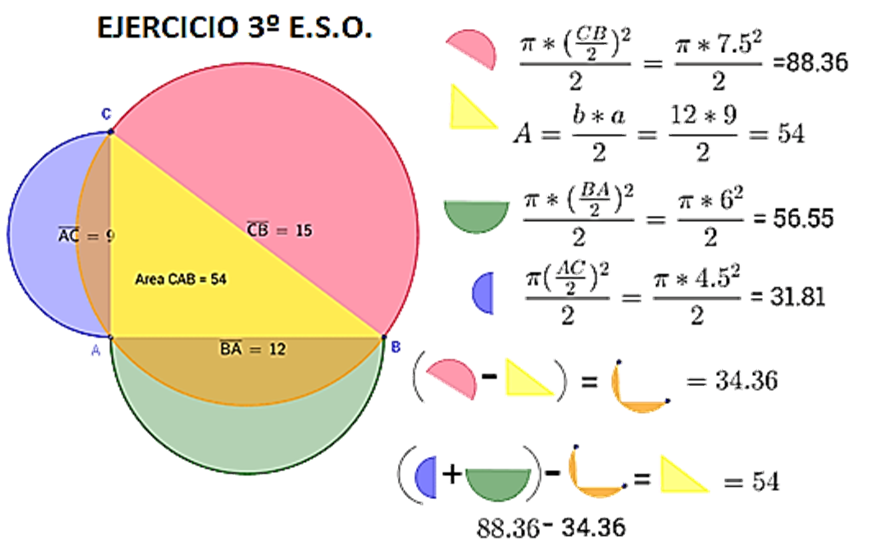
Los antiguos matemáticos griegos adoraban la belleza, la simetría y el orden de la geometría. Hipócrates de Quíos (470 a. C. – 400 a. C.) demostró cómo construir un cuadrado de igual área que una lúnula dada. Una lúnula es una superficie plana en forma de luna creciente , limitada por dos arcos de circunferencia cóncavos. Esta cuadratura de la lúnula es una de las primeras demostraciones matemáticas que se conocen. Resumiendo, Hipócrates demostró que el área de estas lunas se podía expresar de manera exacta como un área rectilínea o “cuadratura”. En nuestro ejemplo, el área conjunta de dos lúnulas (1 y 2) amarillas asociadas con los lados de un triángulo rectángulo coincide exactamente con el área del triángulo. Se adjunta un ejercicio tipo apropiado para el alumnado de 3º ESO.
Para los matemáticos griegos, encontrar la cuadratura equivalía a construir un cuadrado cuya área coincidiera con la de una figura dada utilizando una regla y un compás. Si tal construcción resulta posible, se dice que la figura es “cuadrable”. Los griegos habían logrado la cuadratura de los polígonos, pero las formas curvas resultaban mucho más difíciles.
Hipócrates debe su fama, además, a la primera compilación conocida de trabajos sobre geometría, casi un siglo antes de la de Euclides. Es posible que Euclides se sirviera de algunas de las ideas de Hipócrates para su propia obra, Elementos. La importancia de los escritos de Hipócrates se debe a que proporcionaron un marco común sobre el que construir las matemáticas.
La búsqueda de la lúnula de Hipócrates fue, de hecho, parte del esfuerzo investigador por lograr la “cuadratura del círculo” (es decir, construir un cuadrado cuya área coincidiera con la de una circunferencia dada). Los matemáticos llevaban más de dos mil años tratando de resolver este problema cuando Ferdinand von Lindemann (1882) demostró que era imposible. Hoy sabemos que solo cinco tipos de lúnulas son “cuadrables”.
Hipócrates descubrió tres de ellas; las otras dos se hallaron en la década de 1770.
Bibliografía consultada: The Math Book, Clifford A. Pickover (2009). Proyecto didáctico Vicente Riviére. Ediciones SM, 2002
- Apuntes – Formación (19)
- Biografías (11)
- Boletines (11)
- Curiosidades (23)
- Sin categoría (6)